Lembra do PI? Conheça mais sobre o número irracional infinito

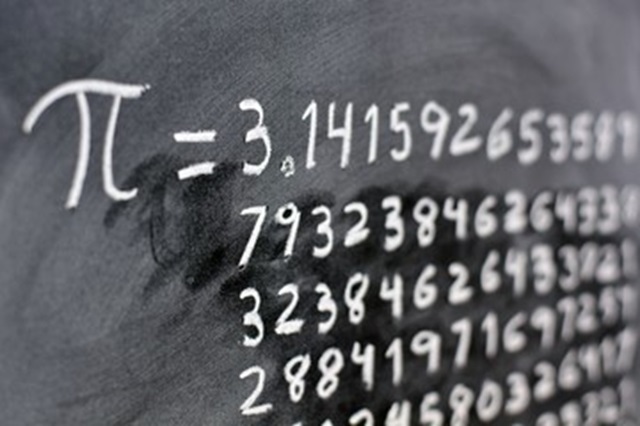
Para quem é apaixonado pela ciência da matemática, este 14 de março é sempre especial. A data, 3/14 (no formato americano), marca o Dia do PI, que significa o resultado da conta de divisão entre o comprimento de uma circunferência e o seu diâmetro. Também definido pela letra grega π, o número 3.14 e contando… pode chegar a ter trilhões de dígitos em seu cálculo. 

O professor do Departamento de Ciências Exatas da Universidade Estadual de Feira de Santana (Uefs), Marcos Grilo, explicou alguns conceitos do número irracional que até hoje não teve seu cálculo preciso revelado por nenhum matemático no mundo. 

“Tome um círculo qualquer e divida pelo seu diâmetro. Essa divisão, essa razão, é sempre constante. E essa constante é o que nós, na matemática, definimos como π. Portanto, o π é a razão da circunferência para o diâmetro de um círculo que vai ser sempre a mesma, é sempre constante”, explicou.

Segundo a história, os primeiros cálculos do número π datam de 1650, pelo papiro de Rhind. Depois, veio Arquimedes, por volta de 240 Antes de Cristo. E em 1873, o matemático britânico William Jones calculou π com 607 casas decimais. Esse cálculo foi feito à mão e levou 15 anos. 

Em 1949, o matemático John Von Neumann conseguiu calcular o π com 2.035 casas decimais, usando um computador. Isso levou 30 horas. O último cálculo de que se tem conhecimento foi feito pelo Google em 2022 com 100 trilhões de casos decimais. Foi realizado em aproximadamente 157 dias.

O número π é irracional e não pode ser expresso como uma fração. A parte decimal dele é infinita e não periódica, o que significa que os dígitos após a vírgula continuam indefinidamente sem repetição. Isso impossibilita calcular π com exatidão, resultando em aproximações, nesse caso, o 3.14.

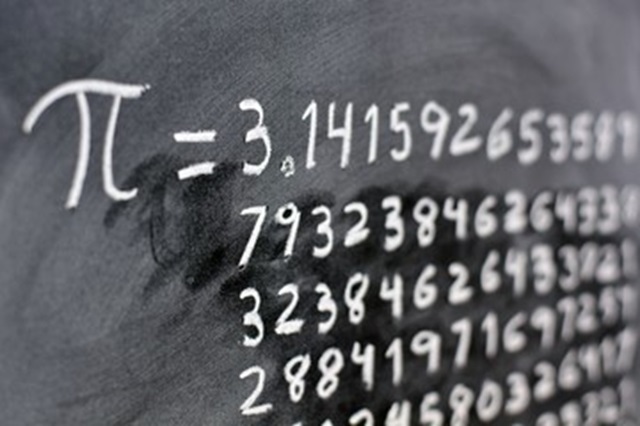
“Os números que vêm após a vírgula, conhecidos como a parte decimal de π, são infinitos e não periódicos, então você tem uma dízima infinita e não periódica, então vão ter infinitos números e você não encontra grupos de números que se repetem. Então, quando você diz que π é 3,1415926535897, isso se prolonga de tal forma que você vai ter infinitos números e você não vai ter periodicidade alguma”.